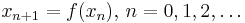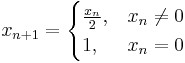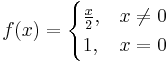Fixed-point iteration
In numerical analysis, fixed-point iteration is a method of computing fixed points of iterated functions.
More specifically, given a function  defined on the real numbers with real values and given a point
defined on the real numbers with real values and given a point 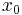 in the domain of
in the domain of  , the fixed point iteration is
, the fixed point iteration is
which gives rise to the sequence 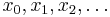 which is hoped to converge to a point
which is hoped to converge to a point  . If
. If  is continuous, then one can prove that the obtained
is continuous, then one can prove that the obtained  is a fixed point of
is a fixed point of  , i.e.,
, i.e.,
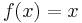 .
.
More generally, the function  can be defined on any metric space with values in that same space.
can be defined on any metric space with values in that same space.
Contents |
Examples
- A first simple and useful example is the Babylonian method for computing the square root of a>0, which consists in taking
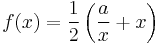 , i.e. the mean value of x and a/x, to approach the limit
, i.e. the mean value of x and a/x, to approach the limit 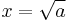 (from whatever starting point
(from whatever starting point 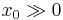 ). This is a special case of Newton's method quoted below.
). This is a special case of Newton's method quoted below.
- The fixed-point iteration
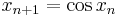 converges to the unique fixed point of the function
converges to the unique fixed point of the function 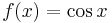 for any starting point
for any starting point 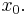 This example does satisfy the hypotheses of the Banach fixed point theorem. Hence, the error after n steps satisfies
This example does satisfy the hypotheses of the Banach fixed point theorem. Hence, the error after n steps satisfies 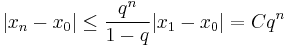 (where we can take
(where we can take 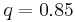 , if we start from
, if we start from 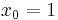 .) When the error is less than a multiple of
.) When the error is less than a multiple of 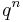 for some constant q, we say that we have linear convergence. The Banach fixed-point theorem allows one to obtain fixed-point iterations with linear convergence.
for some constant q, we say that we have linear convergence. The Banach fixed-point theorem allows one to obtain fixed-point iterations with linear convergence.
- The fixed-point iteration
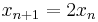 will diverge unless
will diverge unless 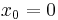 . We say that the fixed point of
. We say that the fixed point of 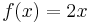 is repelling.
is repelling.
- The requirement that f is continuous is important, as the following example shows. The iteration
converges to 0 for all values of 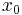 . However, 0 is not a fixed point of the function
. However, 0 is not a fixed point of the function
as this function is not continuous at 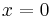 , and in fact has no fixed points.
, and in fact has no fixed points.
Applications
- Newton's method for a given differentiable function
 is
is 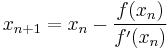 . If we write
. If we write 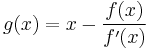 we may rewrite the Newton iteration as the fixed point iteration
we may rewrite the Newton iteration as the fixed point iteration 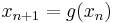 . If this iteration converges to a fixed point
. If this iteration converges to a fixed point  of
of  then
then 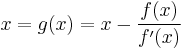 so
so 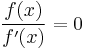 . The inverse of anything is nonzero, therefore
. The inverse of anything is nonzero, therefore 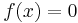 : x is a root of f. Under the assumptions of the Banach fixed point theorem, the Newton iteration, framed as the fixed point method, demonstrates linear convergence. However, a more detailed analysis shows quadratic convergence, i.e.,
: x is a root of f. Under the assumptions of the Banach fixed point theorem, the Newton iteration, framed as the fixed point method, demonstrates linear convergence. However, a more detailed analysis shows quadratic convergence, i.e., 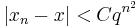 , under certain circumstances.
, under certain circumstances.
- Halley's method is similar to Newton's method but, when it works correctly, its error is
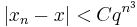 (cubic convergence). In general, it is possible to design methods that converge with speed
(cubic convergence). In general, it is possible to design methods that converge with speed 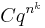 for any
for any 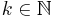 . As a general rule, the higher the
. As a general rule, the higher the  , the less stable it is, and the more computationally expensive it gets. For these reasons, higher order methods are typically not used.
, the less stable it is, and the more computationally expensive it gets. For these reasons, higher order methods are typically not used.
- Runge-Kutta methods and numerical Ordinary Differential Equation solvers in general can be viewed as fixed point iterations. Indeed, the core idea when analyzing the A-stability of ODE solvers is to start with the special case
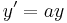 , where a is a complex number, and to check whether the ODE solver converges to the fixed point
, where a is a complex number, and to check whether the ODE solver converges to the fixed point 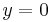 whenever the real part of a is negative.[1]
whenever the real part of a is negative.[1]
- The Picard–Lindelöf theorem, which shows that ordinary differential equations have solutions, is essentially an application of the Banach fixed point theorem to a special sequence of functions which forms a fixed point iteration.
- The goal seeking function in Excel can be used to find solutions to the Colebrook equation to an accuracy of 15 significant figures.[2]
- Some of the "successive approximation" schemes used in dynamic programming to solve Bellman's functional equation are based on fixed point iterations in the space of the return function.[3][4]
Properties
If a function  defined on the real line with real values is Lipschitz continuous with Lipschitz constant
defined on the real line with real values is Lipschitz continuous with Lipschitz constant 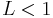 , then this function has precisely one fixed point, and the fixed-point iteration converges towards that fixed point for any initial guess
, then this function has precisely one fixed point, and the fixed-point iteration converges towards that fixed point for any initial guess 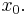 This theorem can be generalized to any metric space.
This theorem can be generalized to any metric space.
The speed of convergence of the iteration sequence can be increased by using a convergence acceleration method such as Aitken's delta-squared process. The application of Aitken's method to fixed-point iteration is known as Steffensen's method, and it can be shown that Steffensen's method yields a rate of convergence that is at least quadratic.
References
- ^ One may also consider certain iterations A-stable if the iterates stay bounded for a long time, which is beyond the scope of this article.
- ^ M A Kumar (2010), Solve Implicit Equations (Colebrook) Within Worksheet, Createspace, ISBN 1-452-81619-0
- ^ Bellman, R. (1957). Dynamic programming, Princeton University Press.
- ^ Sniedovich, M. (2010). Dynamic Programming: Foundations and Principles, Taylor & Francis.
- Burden, Richard L.; Faires, J. Douglas (1985). "2.2 Fixed-Point Iteration". Numerical Analysis (3rd ed.). PWS Publishers. ISBN 0-87150-857-5..
See also
- Root-finding algorithm
- Fixed-point theorem
- Fixed-point combinator
- Banach fixed-point theorem
- Cobweb plot